Cycle Calculations¶
It is also possible to carry out simple thermodynamic cycle calculations with the
CoolProp classes. These calculations are based on the utility classes
CoolProp.Plots.SimpleCycles.StatePoint and
CoolProp.Plots.SimpleCycles.StateContainer, which can be used on their
own as demonstrated below. Note that the utility classes support numerous notations
to access their members and you can chose the one you like best or mix them:
In [1]: from __future__ import print_function
In [2]: import CoolProp
In [3]: from CoolProp.Plots import StateContainer
In [4]: T0 = 300.000; p0 = 200000.000; h0 = 112745.749; s0 = 393.035
In [5]: cycle_states = StateContainer()
In [6]: cycle_states[0,'H'] = h0
In [7]: cycle_states[0]['S'] = s0
In [8]: cycle_states[0][CoolProp.iP] = p0
In [9]: cycle_states[0,CoolProp.iT] = T0
In [10]: cycle_states[1,"T"] = 300.064
In [11]: print(cycle_states)
Stored State Points:
state T (K) p (Pa) d (kg/m3) h (J/kg) s (J/kg/K)
0 300.000 200000.000 - 112745.749 393.035
1 300.064 - - - -
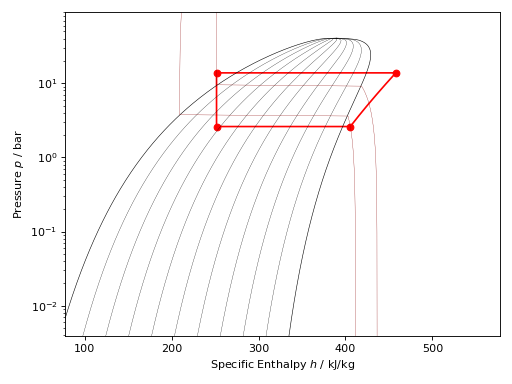
The utility classes were designed to work well with the plotting objects described above and this example illustrates how a simple Rankine cycle can be added to to a \(T,s\) graph, note how the unit conversion is handled:
import CoolProp
from CoolProp.Plots import PropertyPlot
from CoolProp.Plots import SimpleCompressionCycle
pp = PropertyPlot('HEOS::R134a', 'PH', unit_system='EUR')
pp.calc_isolines(CoolProp.iQ, num=11)
cycle = SimpleCompressionCycle('HEOS::R134a', 'PH', unit_system='EUR')
T0 = 280
pp.state.update(CoolProp.QT_INPUTS,0.0,T0-10)
p0 = pp.state.keyed_output(CoolProp.iP)
T2 = 310
pp.state.update(CoolProp.QT_INPUTS,1.0,T2+15)
p2 = pp.state.keyed_output(CoolProp.iP)
pp.calc_isolines(CoolProp.iT, [T0-273.15,T2-273.15], num=2)
cycle.simple_solve(T0, p0, T2, p2, 0.7, SI=True)
cycle.steps = 50
sc = cycle.get_state_changes()
pp.draw_process(sc)
import matplotlib.pyplot as plt
plt.close(cycle.figure)
pp.show()
(Source code, png, .pdf)